Open to work: I am actively seeking full-time opportunities in AI/ML research and development. Feel free to reach out if you'd like to connect!
Warning
Problem: The current name of your GitHub Pages repository ("Solution: Please consider renaming the repository to "
http://".
However, if the current repository name is intended, you can ignore this message by removing "{% include widgets/debug_repo_name.html %}" in index.html.
Action required
Problem: The current root path of this site is "baseurl ("_config.yml.
Solution: Please set the
baseurl in _config.yml to "Education
-
 University of North Carolina, Chapel HillPh.D. in Applied Mathematics, Minor in Statistics & Operations ResearchAug. 2021 - present
University of North Carolina, Chapel HillPh.D. in Applied Mathematics, Minor in Statistics & Operations ResearchAug. 2021 - present -
 University of ChicagoM.S. in Computational and Applied MathematicsSep. 2019 - Mar. 2021
University of ChicagoM.S. in Computational and Applied MathematicsSep. 2019 - Mar. 2021 -
 Shandong UniversityB.S. in Statistics of Mathematics SchoolSep. 2015 - Jun. 2019
Shandong UniversityB.S. in Statistics of Mathematics SchoolSep. 2015 - Jun. 2019
Experience
-
 ByteDanceSeed-AI for Science, Research Scientist InternMay 2025 -- Present
ByteDanceSeed-AI for Science, Research Scientist InternMay 2025 -- Present -
 Argonne National LaboratoryGivens AssociateMay 2023 - Aug. 2023
Argonne National LaboratoryGivens AssociateMay 2023 - Aug. 2023 -
 Deloitte Consulting (Shanghai)Data Visualization & Analyst InternAug. 2018 - Feb. 2019
Deloitte Consulting (Shanghai)Data Visualization & Analyst InternAug. 2018 - Feb. 2019
Activities
Research

Differentiable Optimization
Developed modular convex optimization layer that enables differentiation for any forward solver with seamless integration into neural networks and bi-level optimization tasks, addressing limitation in existing methods that rely on specific forward solvers.

Differentiable Optimization
Developed modular convex optimization layer that enables differentiation for any forward solver with seamless integration into neural networks and bi-level optimization tasks, addressing limitation in existing methods that rely on specific forward solvers.
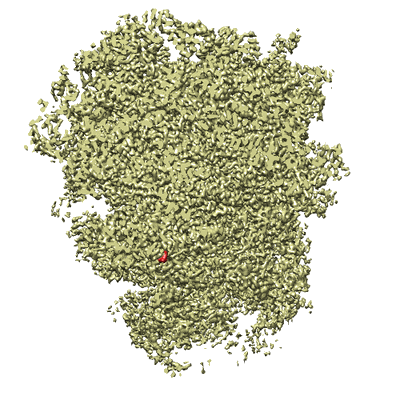
AI-driven Protein Structure Reconstruction
Leading development of PyTorch-based open-source cryo-EM reconstruction software from scratch. Integrating the software to AI foundation models for downstream biology tasks, enabling enhanced protein structure prediction.

AI-driven Protein Structure Reconstruction
Leading development of PyTorch-based open-source cryo-EM reconstruction software from scratch. Integrating the software to AI foundation models for downstream biology tasks, enabling enhanced protein structure prediction.
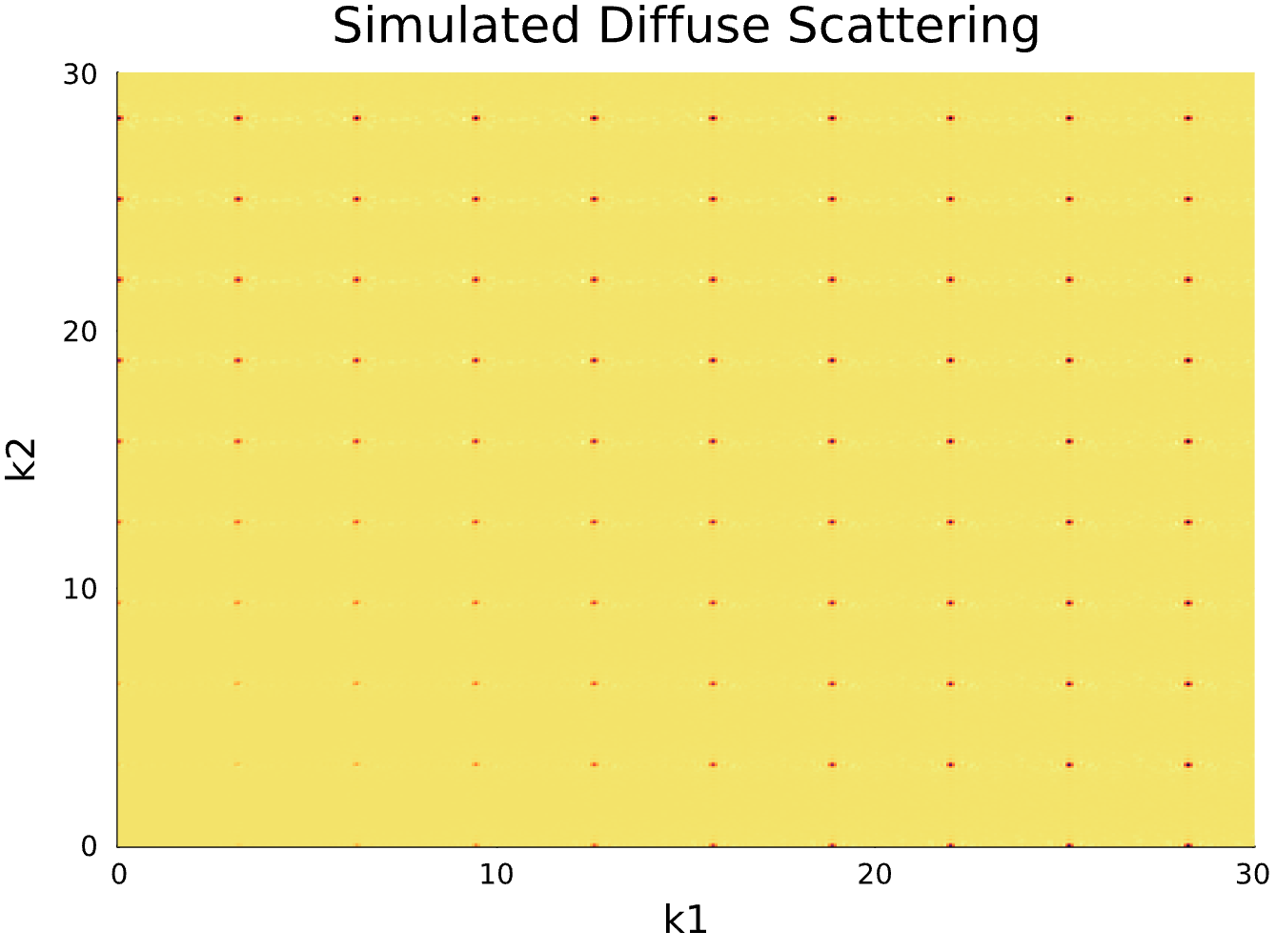
Statistical Model of Crystallographic Disorder
Developed statistical parametric model for analyzing positional and substitutional disorder in crystallography.

Statistical Model of Crystallographic Disorder
Developed statistical parametric model for analyzing positional and substitutional disorder in crystallography.
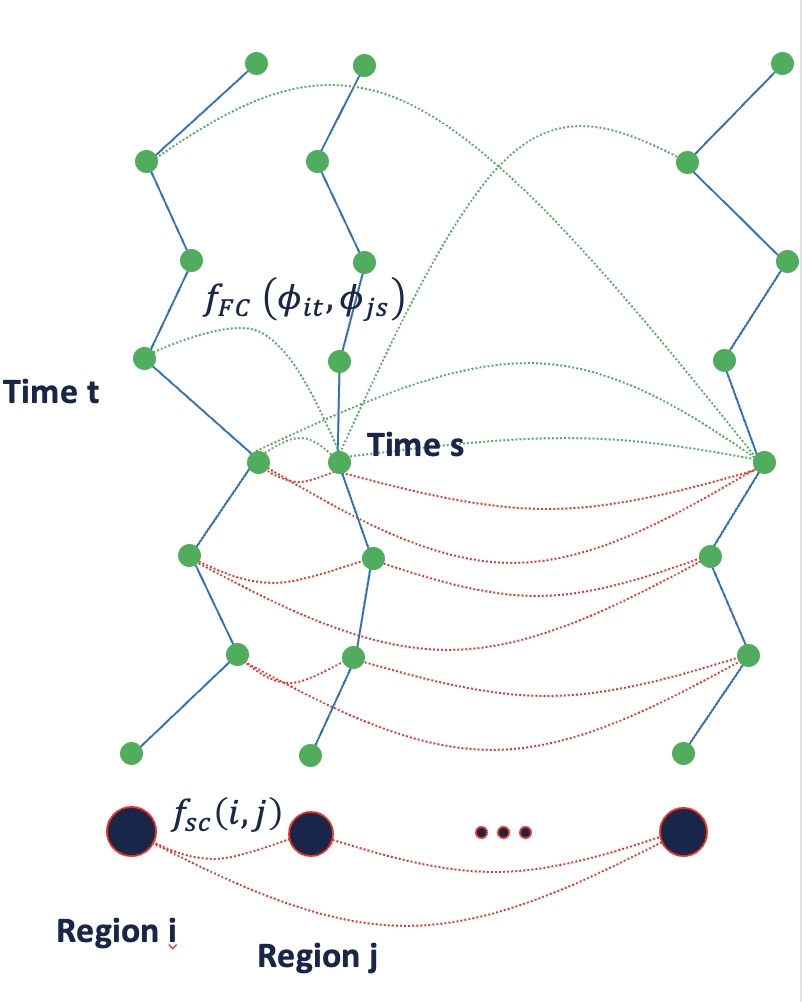
Coupling Structural and Functional Brain Connectome
Developed model for jointly analyzing brain structure connectome (DT-MRI) and the temporal dynamics of individual brain regions (fMRI)

Coupling Structural and Functional Brain Connectome
Developed model for jointly analyzing brain structure connectome (DT-MRI) and the temporal dynamics of individual brain regions (fMRI)
Publications
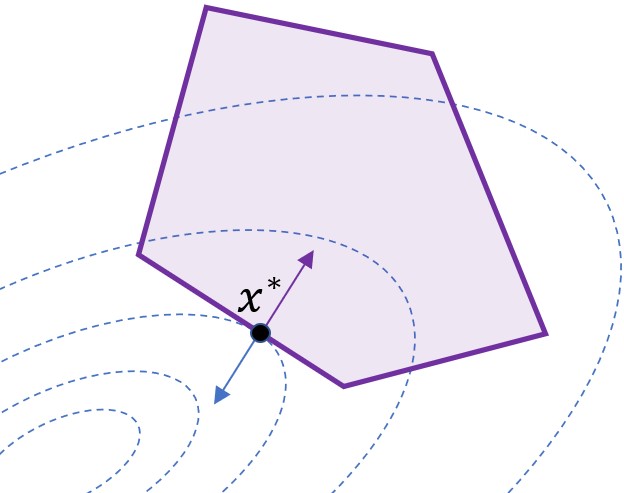
Differentiation Through Black-Box Quadratic Programming Solvers
Connor W. Magoon*, Fengyu Yang*, Noam Aigerman, Shahar Z. Kovalsky (* equal contribution)
NeurIPS 2025
Differentiable optimization has attracted significant research interest, particularly for quadratic programming (QP). Existing approaches for differentiating the solution of a QP with respect to its defining parameters often rely on specific integrated solvers. This integration limits their applicability, including their use in neural network architectures and bi-level optimization tasks, restricting users to a narrow selection of solver choices. To address this limitation, we introduce dQP, a modular and solver-agnostic framework for plug-and-play differentiation of virtually any QP solver. A key insight we leverage to achieve modularity is that, once the active set of inequality constraints is known, both the solution and its derivative can be expressed using simplified linear systems that share the same matrix. This formulation fully decouples the computation of the QP solution from its differentiation. Building on this result, we provide a minimal-overhead, open-source implementation that seamlessly integrates with over 15 state-of-the-art solvers. Comprehensive benchmark experiments demonstrate dQP’s robustness and scalability, particularly highlighting its advantages in large-scale sparse problems.

Differentiation Through Black-Box Quadratic Programming Solvers
Connor W. Magoon*, Fengyu Yang*, Noam Aigerman, Shahar Z. Kovalsky (* equal contribution)
NeurIPS 2025
Differentiable optimization has attracted significant research interest, particularly for quadratic programming (QP). Existing approaches for differentiating the solution of a QP with respect to its defining parameters often rely on specific integrated solvers. This integration limits their applicability, including their use in neural network architectures and bi-level optimization tasks, restricting users to a narrow selection of solver choices. To address this limitation, we introduce dQP, a modular and solver-agnostic framework for plug-and-play differentiation of virtually any QP solver. A key insight we leverage to achieve modularity is that, once the active set of inequality constraints is known, both the solution and its derivative can be expressed using simplified linear systems that share the same matrix. This formulation fully decouples the computation of the QP solution from its differentiation. Building on this result, we provide a minimal-overhead, open-source implementation that seamlessly integrates with over 15 state-of-the-art solvers. Comprehensive benchmark experiments demonstrate dQP’s robustness and scalability, particularly highlighting its advantages in large-scale sparse problems.
